CM3: Cooperative Multi-goal Multi-stage Multi-agent Reinforcement Learning

Context:

• goal-based
• multi-agent
• cooperative (individual reward, but global optimum achieved through cooperation)

Multi-goal multi agent problems are hard to solve, because

• the joint action space is extremely large, and thus efficient exploration is needed
• the multi-goal aspect renders complexifies the credit assignment problem

CM3 solve these with a new framework using 3 synergistic components:

1. The use of a curriculum learning perspective to reframe multi-agent exploration, with a first stage training a single-agent, and a second multi-agent stage using that information to find cooperative solutions faster.
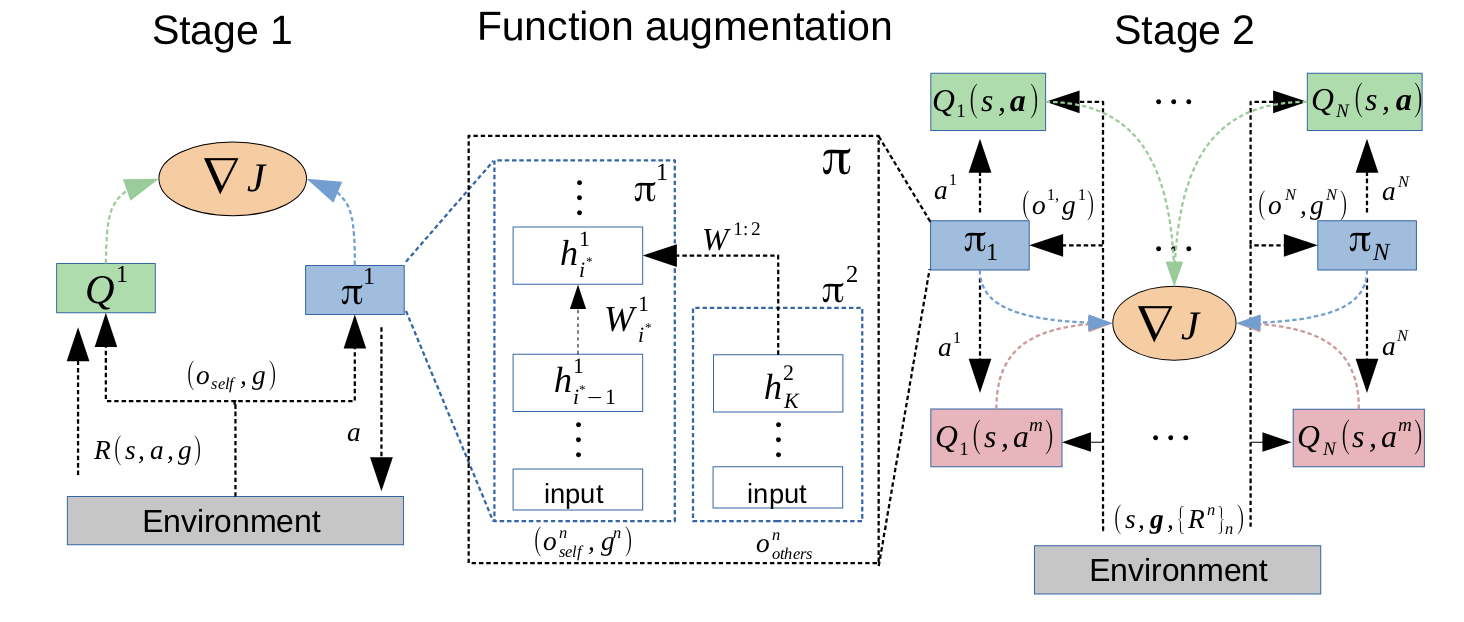
2. A special function augmentation to bridge stages 1 and 2, using the fact that the observations and states can be decomposed in multi-agent environments.
3. A new credit function, which helps with localized credit assignment for multi-goal MARL.

Algorithm §

Credit function §

For a goal $g^n$ and action $a^m$ by agent $m$ is: $Q_n^{\pi }(s,a^m):={\mathbb{E}}_{\pi }\left[{\sum }_{t=0}^{\infty }{\gamma }^t{R}_t^n\right|s_0=s,a_0^m=a^m]$

As this equation can be rewritten in the form of the Bellman expectation equation, the authors explain that it justifies learning this credit function using a standard loss.

They then propose to use this credit function as a critic for a policy gradient multi-goal MARL algorithm, and derive the following gradient to be ascended to maximize our objective: $\begin{array}{c}{\nabla }_{\theta }J(\pi )={\mathbb{E}}_{\pi }[\sum _{m,n=1}^N({\nabla }_{\theta }\log {\pi }^m(a^m|o^m,g^m))A_{n,m}^{\pi }(s,\mathbf{a})]\\ A_{n,m}^{\pi }(s,\mathbf{a}):=Q_n^{\pi }(s,\mathbf{a})-\sum _{{\hat{a}}^m}{\pi }^m({\hat{a}}^m|o^m,g^m)Q_n^{\pi }(s,{\hat{a}}^m)\end{array}$

The sum over $n$ considers all of the agent’s goals, and it updates its policy based on the advantage of $a^m$ over all counterfactual actions it could have taken.

Curriculum §

They propose to tackle the MARL exploration problem by training an agent first individually towards its individual goal, in an environment where the other agents are not present. The first stage of single-agent learning serves as an initialization for the second stage of learning in a MG, helping with the speed of discovery of cooperative solutions.

Warning

The MG has to be simplifiable to a MDP, with a single agent selected as the only one. The authors argue that this is the case in most multi-agent environments used in the literature¹, but this still needs to be considered.

Function augmentation §

To accelerate the training in stage 1, the authors use the fact that an observation can be split into three parts: one component relating to the agent observing, one to the other agents, and one to the global environment. As stage 1 operates in a MDP, the input space of policy and value functions are reduced, so that the information related to other agents is discarded. This information is then re-introduced in stage 2, activating new modules to process the additional input.

Experiments §

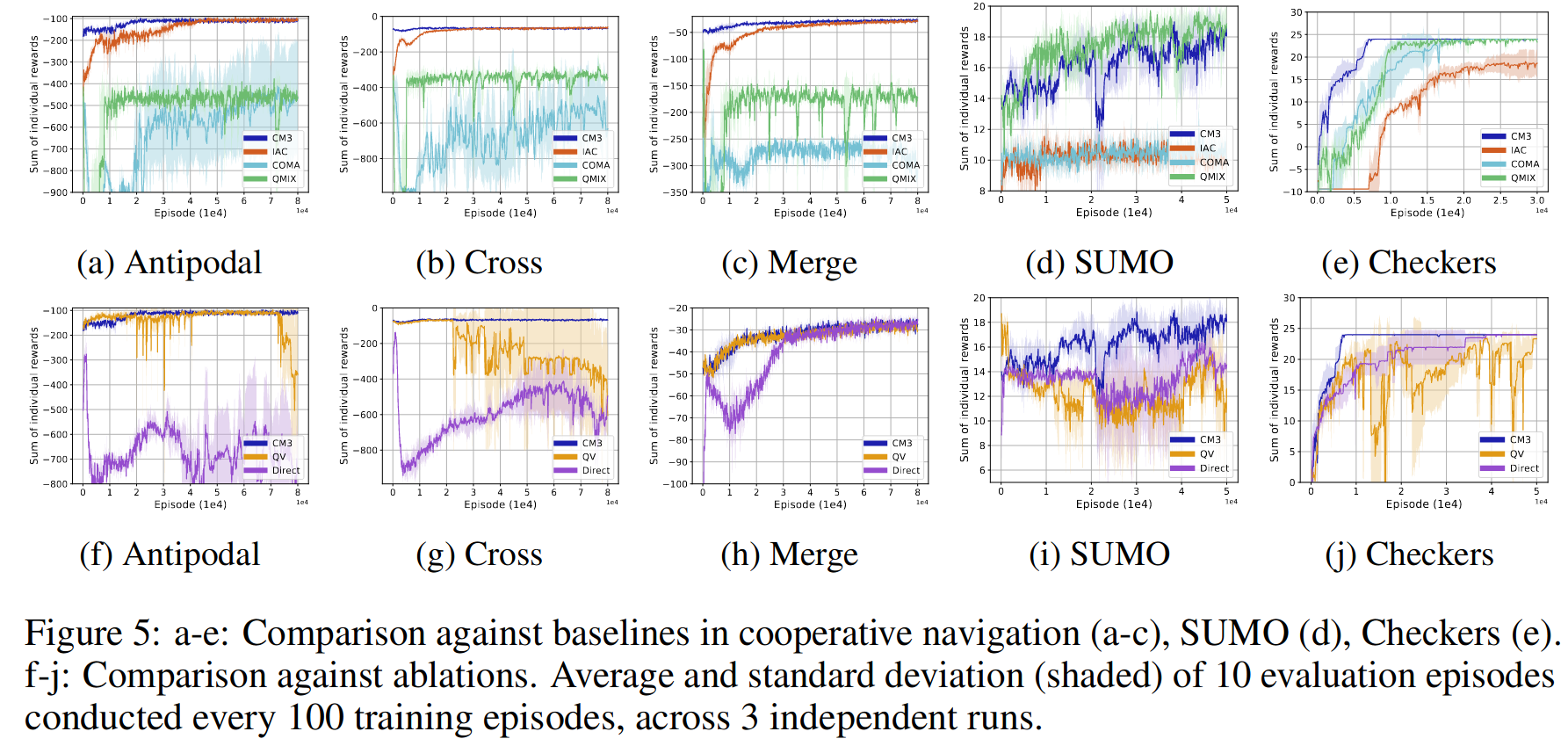
Environments:

• Cooperative navigation (MPE, variants of the scenario used in the MADDPG paper), where each agent only gets an individual reward based on the distance to its designated target.
• SUMO, an autonomous driving environment, in which drivers have to cooperate to reach their personal goal (e.g. perform a double lane merger)
• Checkers, an extension of a pre-existing grid world environment, with a limited field of view and sparse rewards.

Baselines:

• COMA
• QMIX
• Independent Actor Critic (IAC)

Ablations are performed to discover the impact of the curriculum and function augmentation phase (Direct) and the new credit function and multi-goal policy gradient (QV).

Results below show that CM3 is able to solve all environments faster than IAC and COMA, and almost all faster than QMIX. The ablations show that the two-stage method is crucial to improve learning speed and stability. Furthermore, the credit functions and global action-value help with stability and maintaining a cooperative solution.

Footnotes §

1. Exceptions are environments where the objective is defined purely by inter-agent communication. ↩