The paper proposes a new methods for Preference Inference, in which you have to recover a (linear) utility function from reward trajectories. This setup is similar to the policy adaptation phase of Envelope.
Their method, DWPI, learns faster and is more robust to sub-optimal demonstrations than the existing previous works.
Algorithm
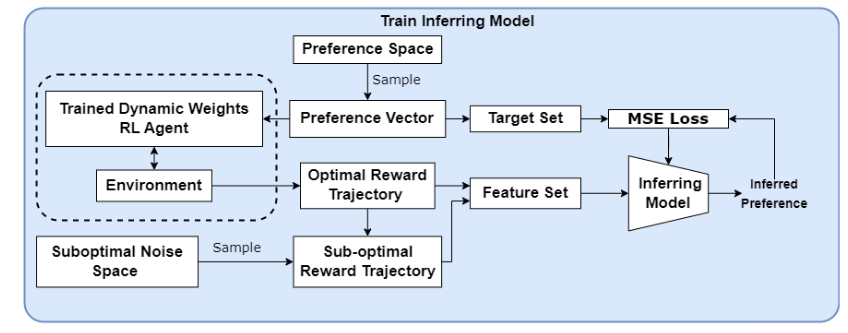
Training phase
By training a MORL (DWRL, Källström and Heintz, 2019) agent, we can generate ground truth (optimal) trajectories and their corresponding weight . They then train a supervised learning model, mapping the average of the obtained reward trajectories to
Note
They use the average reward trajectory, presumably because the trajectories are not fixed-length and thus cannot be used as such as an input to a MLP. This the simplest approach, maybe the model would perform better if it was using more complex representation making full use of the trajectories? This is not listed as potential future work in this paper.
Before being fed to the inferring model, the trajectories are augmented with noise vector and some extra pointless steps, making the model more resilient and enabling it to generalize to sub-optimal examples.
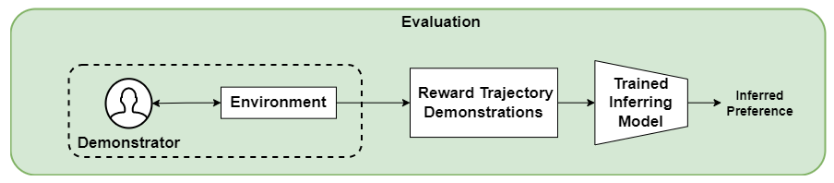
Evaluation phase
For the evaluation, we simply need to generate a reward trajectory from a user, average it, and pass it to the trained inference model which in turn gives us its estimation of the preference vector.
Experiments
Metrics:
- Time efficiency
- MSE between the inferred and ground truth preference vectors
- Distributional Distance (KL-divergence) between inferred and ground truth preference vectors
- Resulting Utility (magnitude of absolute error) between the inferred and true utilities
Environments (discrete observations and actions):
- Convex Deep Sea Treasure
- Traffic (Källström and Heintz, 2019)
- Item Gathering (Källström and Heintz, 2019)
Baselines:
- Projection Method (Ikenaga and Ara, 2018) uses apprenticeship learning and a projection method
- Multiplicative Weights Apprenticeship Learning (Takayama and Arai, 2022)
-> Results show that DWPI is more time efficient and showcases better performances than both PM and MWAL on all environments.