PD-MORL: Preference-Driven Multi-Objective Reinforcement Learning Algorithm

Two versions are proposed:

• one based on double deep Q-network for discrete action spaces
• one based on Twin Delayed Deterministic PG for cont. ones

MO-DDQN minimizes: $L_k(\theta )={\mathbb{E}}_{(s,a,\mathbf{r},s^{\prime },\omega )\sim \mathcal{D}}[(\mathbf{y}-\mathbf{Q}(s,a,\omega ;\theta ){)}^2]$ with $\mathbf{y}=\mathbf{r}+\gamma \mathbf{Q}(s^{\prime },{\sup }_{a\in A}(S_c(\omega ,\mathbf{Q}(s^{\prime },a^{\prime },\omega ))\cdot ({\omega }^{\top }\mathbf{Q}(s^{\prime },a^{\prime },\omega )));{\omega }^{\prime })$, where $S_c$ is the cosine similarity between the preference vector and the Q-values. This term helps with aligning the Q-values with preferences, regardless of the scale of the different objectives.

If a preference vector favors an objective that is correlated to longer episodes, this will create an unbalance in training, with some transitions underrepresented in the experience replay. To prevent that, they use Hindsight Experience Replay, and each transition is also stored with $N$ randomly sampled preferences, along with the original one. Relationship with weight sampling scheme (here they sample weights uniformly)?

Note

Here they talk about using HER in order to homogenize the experience replay. This could probably be equally achieved by using a smarter weight sampling scheme (although using HER is also beneficial for learning).

They also parallelize learning by dividing the preference space into subspaces, and dispatch each of them on a child process.

Warning

This adds a level of exploration, as all subsets (10 by default) are explored independently and randomly. Note that just like the uniform sampling of weight, these subsets are sampled equally which might create a bias in the data as their size is not adjusted during learning.

Because a solution in the PF could not be perfectly aligned with its preference vector, the addition of the cosine similarity in the update scheme could cause a bias. The authors use a multi-dimensional interpolator to project preference vectors onto a normalized solution space. They initialize it by sampling uniformly distributed weights and training an agent with each of them as a single preference and with HER turned off. The obtained solutions are used to get a normalized solution space. The projected preferences are then used for the cosine similarity term.

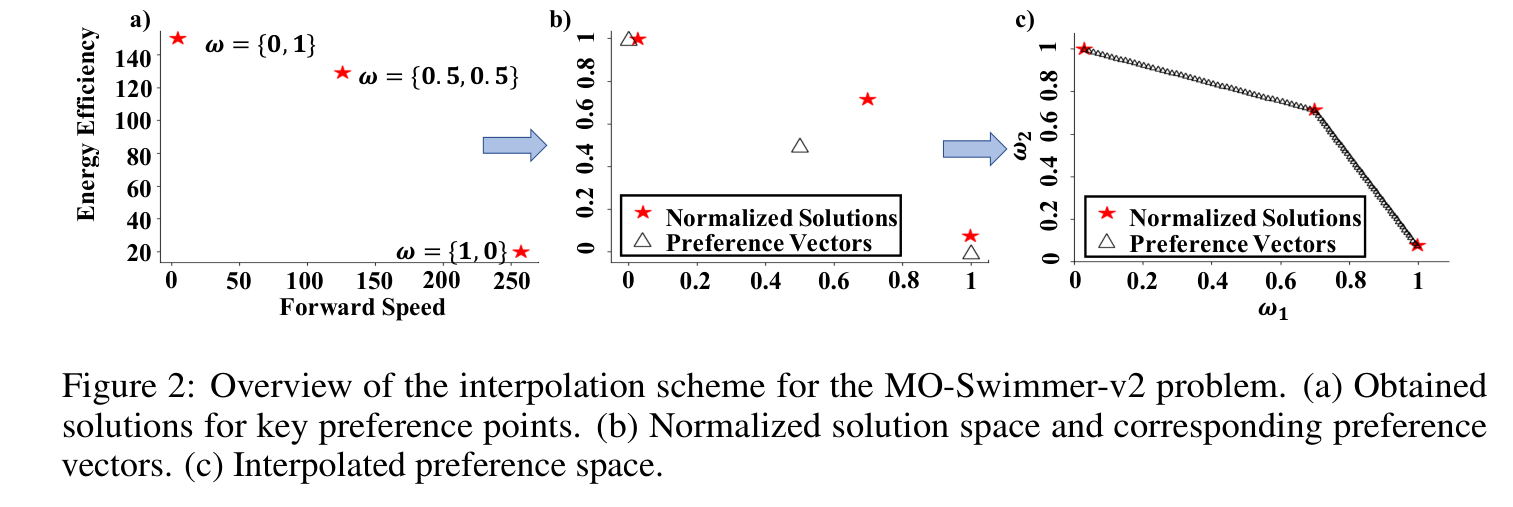
The method can be extended to continuous action spaces using TD3 with small modifications (e.g. incorporation of a directional angle term to the actor’s and critic’s loss to align preferences and Q-values).

Experiments §

Environments:

• Deep Sea Treasure
• Fruit Tree Navigation
• Mo-MuJoCo

Metrics

• Hypervolume
• Sparsity
• CRF1 Yang (2019), defined as the F1 score ($2\frac{\text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}$), with $\text{Precision}=\frac{|B\cap P|}{|B|}$ and $\text{Recall}\frac{|B\cap P|}{|P|}$, $B$ being the set of solutions obtained by the agent for various preferences and $P$ the Pareto front.

DDQN version:

• beats envelope on DST (6.1% increase on HV and 56% lower sparsity), and FTN (HV increase by 10% for d=6, 78% for d=7)

TD3 version:

• Beats PG-MORL and META on almost all MuJoCo environments

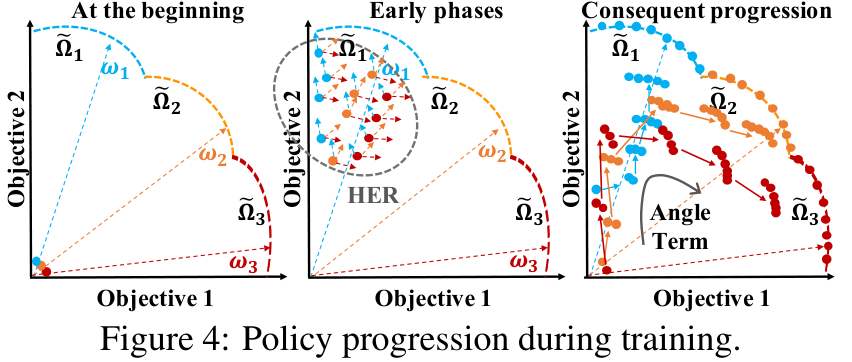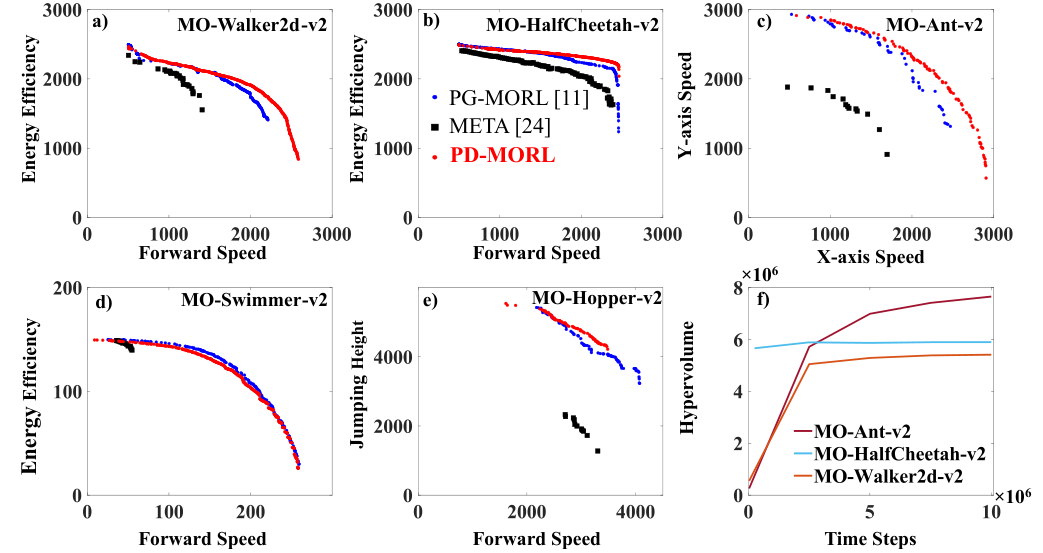Evolution of PD-MORL’s solutions on DST during training	PF comparison for the evaluated methods on MuJoCo environments